ANALISA
INVESTASI TAMBANG
1.1 Latar Belakang ilmu investasi di dunia
pertambangan.
Gambar
Prinsip
Interaktif Analisis Kelayakan Tambang
(Gentry
& O’neil 1987)
![]() Ilmu : geologi, pertambangan, metalurgi, keuangan,
lingkungan
Ilmu : geologi, pertambangan, metalurgi, keuangan,
lingkungan
Kelayakan Investasi Mineral
Tujuan
sarjana tambang (Kelayakan investasi) yaitu :
1.
Memberikan pertimbangan teknis.
2.
Memberikan pertimbangan menyangkut :
§ Design
Penambangan.
§ Metode
destraksi
§ Laju
Penambangan
§ Biaya
Operasi (Operating Cost)
1.2 Karakteristik Industri Pertambangan
- Modal besar.
- Masa pra produksi yang panjang 3 – 12 tahun.
- Berisiko tinggi.
- Cadangan tidak dapat diperbaharui (Non Renueable)
- Mendorong pertumbuhan ekonomi → Multippier Effect.
- Dampak terhadap lingkungan.
- Sifat indestructibility of product → Produk yang didaur ulang.
ad. Modal besar dipengaruhi oleh :
ü Skala
penambangan
ü Lokasi
ü Jenis
bahan galian
ü Teknologi
ü Karyawan/tenaga
kerja.
ad.
Berisiko Tinggi karena :
ü Masa
pra produksi yang panjang.
ü Resiko
politik.
ü Resiko
lingkungan.
ü Resiko
ekonomi.
ü Resiko
geologi
ü Resiko
engineering.
ü Resiko
pasar.
1.3
Fungsi Ilmu Investasi.
Tujuan dilakukannya investasi adalah untuk memperoleh nilai lebih atau
keuntungan di masa depan dari capital atau modal yang di investasikan. Capital
yang dimaksud adalah data berupa :
Capital yang Riil yaitu :
ü Uang
ü Barang
modal
ü Teknologi
ü Tanah
Kapital yang tidak Riil (nyata) yaitu :
ü Hak
paten.
ü Kemampuan
Manajerial.
Dalam bidang pertambangan capital umumnya berupa deposit barang tambang
dan modal, sedangkan menurut Adam Smith, investasi capital umumnya merupakan
investasi utama yang banyak dilakukan oleh individu ataupun perusahaan dalam
rangka meningkatkan tingkat perekonomian mereka.
Keputusan investasi modal mempunyai 2 bentuk tindakan utama yakni :
1.
Mengalokasikan sejumlah modal untuk investasi
proyek tertentu atau untuk menyediakan asset produksi.
2.
Memperoleh sejumlah modal untuk meningkatkan
nilai/pendapatan perusahaan.
Menurut Peter Drucker (Stermole & Stermole), 1996), ada
1.
Mendefinisikan
permasalahan.
2.
Menganalisis permasalahan.
3.
Membuat beberapa alternative solusi.
4.
Memilih solusi yang terbaik.
5.
Membuat keputusan menjadi tindakan yang efektif.
Analisis Investasi ada 3 yaitu :
1.
Analisis
Ekonomi → laba/Rugi
2.
Analisis Fiskal → Pendanaan →
Finansial
ü Modal
sendiri (Individual/Perusahaan)
ü Pinjaman.
ü Saham.
3.
Analisis Itegible → kwantitatif
RUMUS DASAR ANALISIS INVESTASI
2.1 Pengantar
rumus dasar analisis investasi.
Alas an pemberi pinjaman mengenakan bunga kepada peminjam adalah :
![]() Resiko.
Resiko.
![]() Penundaan kesenangan.
Penundaan kesenangan.
![]() Kehilangan Biaya peluang
Kehilangan Biaya peluang
![]() Inflasi
Inflasi
![]() Biaya transaksi.
Biaya transaksi.
ad. 1.
Resiko
Pemberi
pinjaman berhadapan resiko kemungkinan peminjam tidak dapat mengembalikan
pinjamannya.
ad. 2.
Penundaan kesenangan
Dengan
meminjamkan uang pemberi pinjaman dengan peminjam, akan menunda kesenangan
dengan membelanjakan uangnya.
ad. 3.
Kehilangan Biaya peluang
Dengan
adanya kesepakatan pemberi pinjaman dengan peminjam, maka pemberi pinjaman
tidak akan mengambil keuntungan dari peluang yang lain.
ad. 4.
Inflasi
Uang
yang akan dibayarkan kembali dimasa datang mempunyai nilai rendah dari tahun
sebelumnya akibat dari pengaruh inflasi.
ad. 5.
Biaya Transaksi
Akan
terjadi pengeluaran selama diadakan peminjaman untuk kesepakatan peminjaman,
pencatatan dan tugas-tugas administrative lainnya.
Perbandingan
antara biaya tambahan yang dikenakan dengan sejumlah uang yang dipinjamkan
dikenal dengan istilah laju pengembalian bunga (Intereest Rate). Nilai
dinyatakan dalam persentase dengan perhitungan umumnya dalam tahun.
Tingkat
bunga ditentukan pula oleh besarnya persediaan dan permintaan (supply and
demand).
Dalam
ilmu ekonomi terdapat dua jenis bunga yaitu :
![]() Bunga Sederhana (Simple Interest)
Bunga Sederhana (Simple Interest)
Adalah
sejumlah uang yang dibayarkan secara sama tiap tahun sebagai akibat dari
peminjaman uang.
I = P .
n . i
Dimana
:
I = bunga total (%)
P = nilai sekarang (US $) → present
i = laju pengembalian uang (%)
n = periode pengembalian (Tahun)
![]() Bunga Majemuk (Compound Interest)
Bunga Majemuk (Compound Interest)
BC = P (I + i)n
Contoh
soal :
Dik :
P = $
1000
i = 10 %
n = 5
tahun
I = $
1000 . 5 . 10 %
I = $
500/tahun.
BC = $
1000 (1 + 0,1)5
= $ 1610,51
Rumus-rumus
investasi secara umum di dasarkan pada 5 variabel yaitu :
![]() F =
Future (nilai uang pada masa depan) US $.
F =
Future (nilai uang pada masa depan) US $.
![]() P =
Present (Nilai uang sekarang) US $
P =
Present (Nilai uang sekarang) US $
![]() A = Nilai
seragam setiap periode di akhir tahun (Annual =
A = Nilai
seragam setiap periode di akhir tahun (Annual =
US $).
![]() i = Laju
pengembalian uang (Interest Rate = %)
i = Laju
pengembalian uang (Interest Rate = %)
![]() n =
Periode pengembalian (Tahun)
n =
Periode pengembalian (Tahun)
Setiap
pemecahan masalah investasi akan berkaitan dengan 4 dari 5 variabel tersebut. 3
variable diketahui dan satu variable akan dihitung.
Hubungan antar variable
|
Dihitung |
Diketahui |
Factor |
|
F P A A P F |
P, n,
i F, n,
i P, n,
i F, n,
i A, n,
i A, n,
i |
F/Pi,
n P/Fi,
n A/Pi,
n A/Fi,
n P/Ai,
n F/Ai,
n |
Dalam
analisis investasi terdapat 3 type dasar perhitungan analisis yang
memperhitungkan nilai uang antara waktu yaitu :
ü Perhitungan
nilai P yang didasarkan pada nilai F atau A.
ü Perhitungan
nilai F pada P/A
ü Perhitungan
nilai A pada F/P
Untuk lebih memudahkan menganalisis suatu
masalah investasi dan menggambarkan hubungan antar variable maka perlu dibuat
suatu diagram alir kas (ash flow) terhadap waktu.
A =
…….?
F =
1000
i = 5 %
n = 4
tahun
Keterangan
dari gambar diatas yaitu :
![]() Garis horizontal disebut dengan skala waktu dengan
kemajuan waktu bergerak dari kiri ke kanan.
Garis horizontal disebut dengan skala waktu dengan
kemajuan waktu bergerak dari kiri ke kanan.
![]() Tanda anak panah ke bawah → cash
flow negative menandakan aliran kas dan ditempatkan pada akhir periode. Jika
diperlukan perbedaan, maka anak panah keatas menunjukkan aliran cash
positif/penerimaan, sedangkan arah panah kebawah menggambarkan aliran kas
negative/pengeluaran.
Tanda anak panah ke bawah → cash
flow negative menandakan aliran kas dan ditempatkan pada akhir periode. Jika
diperlukan perbedaan, maka anak panah keatas menunjukkan aliran cash
positif/penerimaan, sedangkan arah panah kebawah menggambarkan aliran kas
negative/pengeluaran.
![]() Diagram aliran kas tergantung dari sudut pandang
yang
Diagram aliran kas tergantung dari sudut pandang
yang
![]() Aliran kas merupakan penjumlahan aliran kas positif
(+) dan aliran kas negative (-) pada periode yang sama.
Aliran kas merupakan penjumlahan aliran kas positif
(+) dan aliran kas negative (-) pada periode yang sama.
2.2.1 Rumus investasi dengan bunga majemuk
Penerapan konsep bunga berbunga atau bunga majemuk dalam evaluasi
ekonomi suatu asset atau proyek terdapat dalam enam rumus dasar. Enam (6) rumus
dasar bunga yan dimaksud dalam tabel berikut :
|
Dicari |
Diketa-hui |
Factor perkalian |
Symbol factor fungsinya |
Nama faktor |
|
F P F P A A |
P F A A F P |
(1 + i)n (1 + i)-n (1 + 2)n-1/1 (1 + i)n-1/i(1+i)n i /(1 + i) n-1 |
(F/Pi, n) (P/Fi, n) (F/Ai, n) (P/Ai, n) (A/Fi, n) (A/Pi, n) |
Single payment compound factor. Single payment present worth factor. Uniform series. Ompound amount factor/uniform series Present worth factor sinking fund deposite ROC Capital Recovery Factor |
3.2.2.
Single
Payment Compound Amount Factor.
Perhitungan untuk mendapatkan nilai F dengan P, diketahui pada n periode
dan laju bunga/periode. Jika sejumlah P berada pada titik waktu tertentu dan I
% adalah laju bunga per periode, maka jumlah P tersebut akan berkembang di masa
datang menjadi P + Pi = P(1 + i) pada akhir periode pertama, pada akhir periode
kedua berubah menjadi P (1 + i) (1 + i)
= P (1 + i)2. Pada akhir period eke tiga menjadi P (1 + i)2.(1
+ i) = P (1 + i)3 dan pada akhir periode n akan menjadi
Nilai
dari (1 + i)n disebut dengan Single Payment Compound Amount Factor. Symbol yang
terkhir untuk factor ini adalah F/Pi%, n, sehinga persamaan diatas dapat
diganti dengan
F = P
(F/Pi%, n)
Dalam
bentuk diagram alir kas
![]() UNIFORM
V-SERIES COMPOUND AMOUNT FACTOR (Pembayaran Uniform Series)
UNIFORM
V-SERIES COMPOUND AMOUNT FACTOR (Pembayaran Uniform Series)
F =
A(F/A i%, n)
Misal :
i =
¾ %/tahun
n =
5 tahun
A =
$ 100
F/P =
1,038 F/A = 5,076
P/F = 0,9633 P/A
= 4,889
A/F = 0,1970 A/G
= 1,986
A/P = 0,2045 P/G
= 9,712
Þ
F = A(F/A i%, n)
= $ 100 (5,076) = $ 507,6
Þ
Perhitungan
untuk mendapatkan nilai F pada n periode dari sekarang berdasarkan penjumlahan
dari A dengan laju bunga i per periode.
Dimana :
 = (F/A i%,n) = Uniform
series ompound amount fator yang telah didistribusikan.
= (F/A i%,n) = Uniform
series ompound amount fator yang telah didistribusikan.
![]() SINKING
FUND – DEPOSIT FACTOR (Simpanan Teratur)
SINKING
FUND – DEPOSIT FACTOR (Simpanan Teratur)
Perhitungan
untuk mendapatkan nilai A selama n periode berdasarkan P dengan laju bunga i
per periode.
![]()
» Sinking – Found Deposite Factor yang telah
dibatasi.
![]() CAPITAL
– RECOVERY FACTOR (Penerimaan Teratur).
CAPITAL
– RECOVERY FACTOR (Penerimaan Teratur).
Perhitungan
untuk mendapatkan nilai A selama n periode berdasarkan P dengan bunga i per
periode.
Dimana
:
![]() UNIFORM
SERIES PRESENT – WORTH FACTOR
UNIFORM
SERIES PRESENT – WORTH FACTOR
(Nilai sekarang Pembayaran Uniform)
Perhitungan
untuk mendapatkan P berdasarkan penjumlahan A selama n periode dengan laju
bunga i per periode.
![]() ARITHMATIC
GRADIENT SERIES.
ARITHMATIC
GRADIENT SERIES.
Salah
satu situasi yang sering muncul dalam analisis investasi adalah peningkatan
atau penurunan pendapatan/biaya.
Secara
gradient selama periode. Anlisis peningkatan/penurunan ini disebabkan oleh
factor Ekskalasi (kenaikan) yang dikarenakan oleh efek inflasi, persediaan
(supply), dan permintaan (demand), dan analisis ekonomi, permasalahan ini
disebut dengan “Arithmatic Gradient Series”.
Ilustrasi
Diagram alir.
Dimana
: B = Gradient series
g = Gradient konstan
Untuk
menentukan pemecahan persoalan “Arithmatic Gradient Series” diubah menjadi
“Uniform Series Compound”.
Formula
:
A = b + g (A/G i%, n)
Contoh
:
Diketahui ;
ü
Gradient series pertama, B = 1100
ü
Arithmatic gradient, g = 100
ü
Laju bunga, i = 8 % per periode
ü
Umur proyek, n
= 10 tahun.
Pertanyaan
:
Tentukan
nilai A = ….. ?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A =
1100 + 100 (A/G 8%, 10)
= 1100 + 100 (3,871)
= 1100 + 387,1
= 1487,1
![]() BUNGA
EFEKTIF
BUNGA
EFEKTIF
Biasanya “Discount Rate” dinyatakan dalam penyatuan
biaya nominal tiap tahun jika investasi dibungakan tiap tahun (Annual
Compounding) bunga nominal dan bunga efektif ( j
& i ) akan sama besar. Jika investasi dibungakan pada selang waktu yang
kurang dari setahun, maka bunga efektif akan sedikit lebih besar daripada bunga
nominal. Hubungan berikut dapat dipakai untuk menghitung bunga efektif. Jika
bunga nominal dan frekuensi pengadaan diketahui.
Formula :
dimana :
i = bunga efektif, %
j = bunga nominal, %
m = periode pengembalian
Contoh :
Sebuah perusahaan kartu kredit membebankan suku bunga sebesar 1,375% per
bulan pada saldo semua rekening belum terbayar. Tingkat suku bunga tahunan
menurut mereka adalah 12 (1,375%) = 16,5%. Berapakah suku bunga efektif per
tahun yang dibebankan oleh perusahaan.
Jawab :
= 0,1781
= 17,81%
Soal :
Uang sebesar Rp. 1.000.000,-, jika disimpan selama 8 tahun dengan
tingkat bunga 10% per tahun akan menjadi ?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
F = P(F/A i%, n)
= Rp.1.000.000, (F/A 10%, 8)
= Rp. 1.000.000 (2,1436)
= Rp. 2.143.600,-
Atau ;
Soal :
Uang Rp. 1.000.000,- diterima 8 tahun yang akan datang dengan tingkat
bunga 10%, berapa nilainya pada saat sekarang.
P = F(P/F 10%, 8)
= Rp. 1.000.000,- (0,4665)
= Rp. 466.500,-
Soal :
Jika kita menginginkan jumlah tabungan sebesar Rp. 1.000.000,- di akhir tahun ke 8, tentukan
berapa yang harus di tabung per tahun dengan tingkat suku bunga 10%.
Diketahui :
F = Rp. 1.000.000,-
i = 10%
n = 8 Tahun
A = F (A/F i%, n)
= Rp. 1.000.000,- (A/F 10%, 8)
= Rp. 1.000.000,- (0,0874)
= Rp. 87.400,-
Soal :
Jika kita meminjam uang di Bank Rp 1.000.000,- dan ingin melunasinya
selama 10 tahun dengan tingkat suku bunga yang dibebankan oleh Bank sebesar 15%
per tahun. Tentukan berapa yang harus dibayarkan setiap tahunnya.
Jawab :
A = P (A/P i%, n)
= Rp 1.000.000,- (0,1993)
= Rp 199.300,-
ALIRAN KAS
(CASH FLOW)
Aliran kas adalah sejumlah uang yang masuk (pendapatan/cash in) atau
yang keluar (pengeluaran/investasi/cash out) dari suatu kegiatan/proyek dalam
suatu periode waktu tertentu.
![]()
![]()
![]() Arti penting dari aliran kas (Cash Flow)
Arti penting dari aliran kas (Cash Flow)
Ø
Akuntansi laba bukan kas bersih.
Ø
Investor →
Laporan kas
Ø
Dengan Cash Flow → alternative investasi
(pembayaran peminjaman)
Contoh :
Suatu perusahaan mendapatkan kontrak pembuatan perahu yang harus
dikerjakan selama lima tahun, dimana pembayaran perahu 40 % diakhir tahun-2, 40
% di akhir tahun ke-4, dan sisanya 20 % dibayarkan pada akhir tahun ke-5.
Dimana perusahaan penerima proyek mampu menyelesaikan kontrak 20 % disetiap
tahunnya dan biaya yang dibutuhkan 20 %per tahun.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Komponen Aliran Kas
Komponen Aliran Kas
1.
INITIAL CASH FLOW (Aliran kas awal/Pendahuluan)
2.
OPERATIONAL CASH FLOW (Aliran Kas Operasional)
3.
TERMINAL CASH FLOW (Aliran kas di akhir/sisa)
KRITERIA EVALUASI PROYEK
4.1.
Kriteria
Evaluasi Proyek
ü
NPV : Net
Present Value : Nilai sekarang
ü
BCR : Benefit
Cost Ratio : Ratio antara pendapatan
& investasi
ü
POT : Pay Out
Time : Waktu pengembalian
ü
ROR : Rate Of
Return : Break Event
NPV = 0 = Investment = Income
Salah satu elemen penting dalam mengevaluasi
investasi atau proposal investasi.
1. Proposal Invesrasi Independen
(Individual/tidak tergantung)
2. Proposal
Investasi Dependen (Mutually Exlusive)
3. Proposal
Investasi Kontigensi
1. Proposal Investasi Independen
(Individual/Tidak tergantung)
Pemilihan suatu proposal investasi tidak
mempengaruhi proposal investasi yang lain.
Contoh : Proposal pemilihan system keamanan gudang bahan peledak
2. Proposal
Investasi dependen (Mutually Exlusive)
Adalah pemilihan suatu proposal investasi yang
mempengaruhi pemilihan proposal investasi yang lainnya.
Contoh : Proposal pembuatan jalan tambang akan
mempengaruhi pemilihan proposal alat muat dan alat angkut.
3. Proposal
Investasi Kontigensi
Adalah pemilihan proposal investasi akan berakibat
diperlukannya suatu proposal investasi lain yang mendukung atau komplementer.
Contoh : Proposal pembelian Dump Truck akan
menyebabkan diperlukannya proposal pembelian ban.
![]() Prinsip penting dalam mengevaluasi proposal
investasi adalah :
Prinsip penting dalam mengevaluasi proposal
investasi adalah :
ü
Keuntungan besar lebih baik daripada keuntungan
kecil.
ü
Keuntungan yang diperoleh cepat lebih baik daripada
yang diperoleh lambat.
ü
Hasil evaluasi harus konsisten dan realistis.
4.2. Dasar Perhitungan Evaluasi Proyek
Terdapat 2 klasifikasi investasi yang umum
digunakan (Stermole & Stermole, 1996), yaitu :
1. Investasi yang memproduksi pendapatan
(Revenue – Producing Investement Alternatives)
2. Investasi
yang memproduksi jasa/layanan
(Service – Producing Investement Alternatives)
1. Investasi yang memproduksi pendapatan
(Revenue – Producing Investement Alternatives)
Dalam investasi yang memproduksi pendapatan yang dicari
adalah alternative proyek yang menghasilkan pendapatan terbesar dan amat besar
yang digunakan adalah analisis nilai pendapatan (Net Value Analisis).
2. Sedangkan
dalam investasi yang memproduksi jasa pelayanan yang dicari adalah Alternative
proyek yang menghasilkan nilai biaya terkecil/minim dan analisis yang digunakan
adalah Analisis Biaya (Cost Analisis).
Dalam evaluasi investasi ada 3 persamaan yang
sering digunakan yaitu :
1. Present Worth (PW) Equation
PW Cost = PW Income/Revenue
Membandingkan pendapatan dan biaya di awal umur proyek.
2. Annual
Worth (AW) Equation
Equivalen Annual Cost = Eq – Annual Cost
Equivalen Annual Revenue = Eq – Annual Revenue
Dimana membandingkan pendapatan dan biaya secara series tiap tahunnya.
3. Future
Worth (FW) Equation
FW cost = FW revenue
Membandingkan antara pendapatan dan biaya di akhir umur proyek.
Biaya (cost) = Out Flow
Pendapatan (Revenue)
Biaya (Cost) adalah pengeluaran termasuk biaya operasi langsung dan
tidak langsung, pembayaran utang investasi dan lain-lain.
Dalam aliran kas biaya merupakan aliran kas negative (Out Flow).
Sedangkan pendapatan (Revenue) adalah pendapatan hasil penjualan, nilai
sisa atau “Savage Value”, Hak Paten, Piutang jasa, dan lain-lain.
Aliran kas pendapatan merupakan aliran kas positip (In Flow).
Tugas 1 :
Cari yang termasuk di dalam biaya langsung dan biaya tidak langsung.
Jawab :
Ø
Biaya Langsung (Direct Cost) adalah biaya-biaya
yang secara beralasan dapat diukur dan dialokasikan ke suatu keluaran atau
kegiatan kerja tertentu diantaranya :
ü
Investasi
ü
Operating Cost
ü
Pembelian Alat
ü
Gaji Karyawan
Ø
Biaya Tidak Langsung (Indirect Cost) adalah
biaya-biaya yang sulit untuk dimasukkan atau dialokasikan ke suatu keluaran
atau kegiatan kerja tertentu, seperti :
ü
Perbaikan
ü
Royalty
ü
Bunga Pinjaman
ü
Asuransi
ü
Ongkos-ongkos Jamuan untuk tamu-tamu.
Contoh soal :
Sebuah investasi penyewaan rumah mengharapkan hasil US$ 2,000/tahun.
Biaya untuk 10 tahun yang akan datang dan mengharapkan nilai sisa US$ 25,000
per 10 tahun. Berapa yang dapat dibayarkan untuk property ini sekarang, jika
Return Before Taxes sebesar 12 %.
C=… I=$2,000
PW Cost = PW Income
=
A (P/A 12%, 10) + L (P/F 12%, 10)
=
$ 2,000 (5,650) + $ 25,000 (0,3220)
=
$ 11,300 + $ 8,050
=
$ 19,350 → jumlah yang harus dibayarkan pada thn 0
FW
C (F/P 12%, 10) = $ 2,000 (F/A 12%, 10) + $ 25,000
C (3,106) = $ 2,000 (17,549) + $ 25,000
C = $ 19,349.
AW = …. ?
AW Cost = AW Revenue
C(A/P 12%,10) = $ 2,000 + $ 25,000
(A/F 12%, 10)
C (0,1770) = $ 2,000 + $ 25,000 (0,057)
= $ 2,000 + $
1,425
= $ 19,350
Cost :
ü
PWE
ü
FEW
ü
AWE
ROR/IRR = Rate Of Return/Internal Rate Of Return
ROR/IRR = Tingkat suku bunga yang menyebabkan nilai
NPV=0/NAV=0
NPV = NPVPenerimaan – NPVPengeluaran
= 0
NPVPenerimaan = NPVPengeluaran =
ROR
Besarnya ROR dari pihak investor memperhitungkan
setiap tahun berdasarkan pada investasi yang tidak Amertisasi (nilai investasi
berdasarkan pinjaman manajemen)
Contoh : Biaya pengembangan proyek (Development).
Pengertian ROR bukan hanya sejumlah nilai yang
diterima dan investasi setiap tahun tetapi sejumlah nilai yang diterima dari
investasi tidak Amertisasi setiap tahunnya.
Perhitungan yang umum digunakan dalam perhitungan
ROR adalah dengan menggunakan :
Keuntungan dari metode perhitungan Arrange ROR adalah :
1. Perhitungan
Sederhana
2. Dapat
memperoleh informasi Akuntansi yang lebih cepat.
3. Memperlihatkan
langsung besar ROR yang dibutuhkan dalam suatu proyek Investasi.
Kelemahan Metode ROR adalah :
1. Perhitungannya
berdasarkan keuntungan bukan pada nilai actual aliran kas.
2. Jangka
waktu dari keuntungan tidak diperhitungkan
![]() Cumulative Cash Position Diagram
Cumulative Cash Position Diagram
Adalah prinsip investasi dan bunga ayng belum di
Amertisasi oleh Revenue seperti profit, nilai sisa simpanan dan In Flow lainnya
atau dana yang masuk.
Cash Flow Cumulative Position Diagram dimulai
biaya/Out Flow terus berjalan sampai mencapai posisi nol pada akhir proyek.
Keuntungan dari penggunaan Cumulative cash Position Diagram adalah :
Ø
Dapat menggambarkan dengan lebih baik daripada
penjelasan yang berupa kumpulan data-data ataupun diagram.
Contoh :
Untuk suatu investasi $ 10,000 sekarang, seseorang menerima pendapatan $
2,638 pada akhir tahun ke-5, umur proyek 5 tahun, dengan L = 0
Pertanyaan ;
Hitung ROR dan Diagram CCP
Solusi :
AWE = $ 10,000 (A/P 0%, 5) = $
2,638 → i = … ?
5 % = $ 10,000 (0,2310) =
$ 2,310
10 % = $ 10,000 (0,2638) =
$ 2,638
Jadi ROR = 10 %
Cara
mendapatkan nilainya ;
ü
- 10,000 + 10% (-10000) = -11000 + (-1000)
= -11000
-11000 + 2638 =
8362
ü
-8362 + 10% (-8362) = -8362 + (-836,2) = -9198,2
o
-9198,2 + 2638 = -6560,2
ü
-6560,2+10% (-6560,2) = -7216,22
·
-7216,22+2638 = -4578,22
ü
-4578,22 + 10%(-4578,22) = -5036,042
-5036,042+2638 = -2398,042
ü
-2398,042+10%(-2398,042) = -2368,0
-2368 + 2368 = 0
Hitung
nilai IRR dari proyek yang mempunyai aliran kas sbb:
|
Tahun |
0 |
1 |
2 |
3 |
4 |
5 |
|
Aliran Dana |
-100 |
20 |
30 |
20 |
40 |
40 |
i = 10 %
NPV =
-100+20(P/F10%,1)+30(P/F10%,2)+20(P/F10%,3)+40(P/F10%,4)+40(P/F10%,5)
=
-100 + 20 (0,0991) + 30 (0,8264) + 20 (0,7513) + 40 (0,6830) + 40 (0,6209)
=
-100 + 18,182 + 24,79 + 15,026 + 27,32 + 24 836
=
$ 10,12
i = 15 %
=
-100 + 17,392 + 22,683 + 13,15 + 22,872 + 19,8808
NPV =
-100 + 20 (0,8691) + 30 (0,7561) + 20 (0,6573) + 40 (0,5718) + 40 (0,19720
=
-4,07























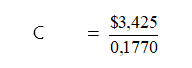




Show Conversion Code Hide Conversion Code Show Emoticon Hide Emoticon